If you just signed up for a Calculus 1 class, you’re probably wondering what Calculus 1 is, as well as what is taught in the class. Maybe you’ve even heard horror stories about Calculus and you’re concerned about taking it yourself. Well allow me to dispell those concerns and explain what Calculus 1 is and you can expect to learn from the course.
What Is Calculus 1?
Calculus 1 is an introductory course in Calculus that covers the basic principles of differential and integral Calculus. It is usually taken by students who are majoring in mathematics, science, engineering, or related fields. In this course, students learn how to calculate derivatives of functions, solve optimization problems, and integrate functions.
Some of the topics that are covered in Calculus 1 include limits, derivatives, applications of derivatives (such as optimization and related rates), integrals, and the Fundamental Theorem of Calculus. Calculus 1 is a foundational course for higher-level mathematics courses and is often a requirement for many science and engineering programs.
What Will I Learn In Calculus 1?
Calculus 1 is also known as Differential Calculus, so what you should expect to learn, roughly 75%, will be Differentiation. But what is Differentiation? And what is the other 25% of what you learn?
First, differentiation is when you find the derivative of a function. The derivative shows us the instantaneous rate of change or the slope at any given point. Second, the other 25% is split between reviewing functions (10%) at the beginning of the course and Integrals (15%) at the end of the course.
Allow me to go more in-depth…
The First 10% – Reviewing Functions
What does this first 10% of the course, reviewing functions, look like? There are four main types of functions that you have to be well acquainted with going into Calculus 1: Exponential functions, Logarithmic functions, Trigonometric functions, and Polynomial functions. Luckily, the first thing typically done in a Calculus 1 course is to review these four functions.
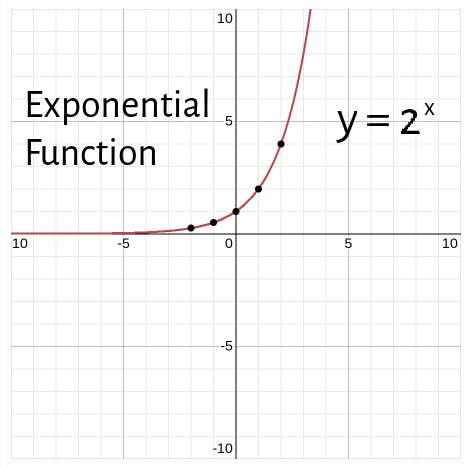
Exponential Functions
The variable ‘x’ is the exponent on a constant base. Exponential Functions are commonly used to represent natural phenomena such as bacteria growth or radioactive decay.
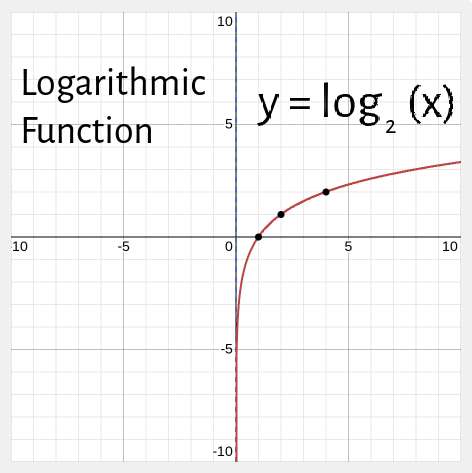
Logarithmic Functions
The variable ‘x’ is the inverse of the exponent. Log Functions help condense extremely large or extremely small values into something more manageable. Log Functions also represent natural phenomena.
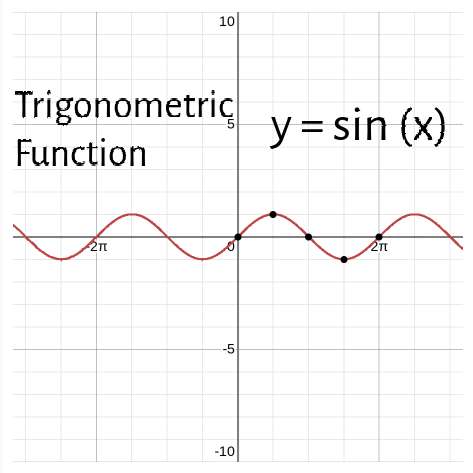
Trigonometric Functions
Also known as circular functions, related right-angle triangles. Trig Functions can be tough and knowing them is vital to pass Calculus. Make sure you memorize your unit circle!

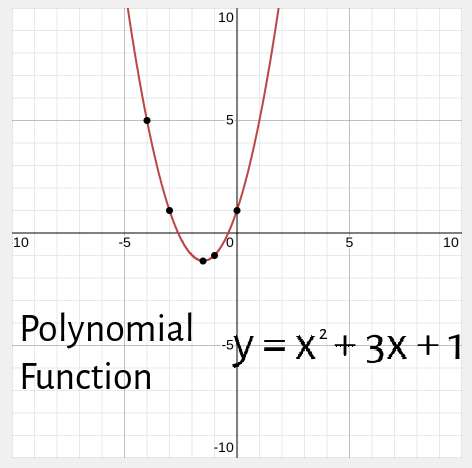
Polynomial Functions
Polynomials are perhaps the most broadly used in real-life applications. They are used in all manner of sciences, economics, and business, from modeling markets to modeling the trajectory of projectiles. A common type of polynomial is a quadratic function, such as the one graphed below.
Side Note:
Your Professor will likely cover more than these four functions, including transformations of functions, combinations of functions, ratios of functions, and more.
The goal that Universities have for students by the end of Calculus 1 is that they can look at a complex polynomial function, analyze it to find domain, range, intercepts, asymptotes, mins, max’s, etc., and sketch a pretty accurate graph.
You should already be able to do this pretty well with linear functions, as they are very basic. However, the more complex the function is, the more complex the graph will be, and the harder it will be to analyze that function and sketch its graph.
The Core 75% – Differentiation
Differentiation is the core of what you learn in Calculus 1. Differentiation is something you do to a function to find that function’s derivative. Once you’ve found the derivative, you can use it in all sorts of interesting ways. Here are the answers to all the questions you’ll have, but may not know to ask.
What is a Derivative?
I’ve been struggling to try to come up with a good definition for a derivative that someone could understand easily, even as a new concept. Rapid Tables seemed to have a pretty good definition:
The derivative of a Function is the ratio of the difference of function value f(x) at points x+Δx and x with Δx, when Δx is infinitesimally small. The derivative is the function slope or slope of the tangent line at point x.
If that makes sense to you, great. If not, let’s look at it like this.
We have a function graphed below:
f(x) = x2
We take three inputs: -1, 0, and 2
We can find the output by simply plugging the inputs into the original function. The result is three points. But what if I want to find the instantaneous slope at each of these points?
First, we find the derivative of the function which is 2x (don’t worry about how to do this just yet). Then, we plug the original input into the derivative:
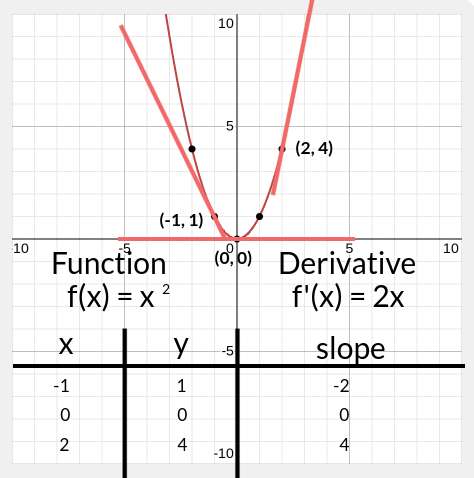
If you’d like to know more about the concept of the derivative, you can click here to go through the section for Derivative definition and basic rules on Khan Academy.
How Do I Find The Derivative Of A function?
The derivative is found in many different ways, but we typically use basic Derivative rules to find it. These are the power rule, the product rule, the quotient rule, and the chain rule.
I’m not going to explain all of these thoroughly, especially not the chain rule because it’s too complex for this overview. However, I will talk a little about the power rule.
The power rule is the first derivative rule you learn and you’ve already seen an example of that with the last graph: f(x) = x2. It’s actually very easy to understand:
The Power Rule
Take the power of the variable in the function, the variable is ‘x’ and the power is ‘2’ and move the power down by the coefficient of the variable. If there is already a coefficient, then multiply the power by the coefficient and that will be the new coefficient. Then you subtract the power by ‘1’ and that’s your derivative!
Let’s look at it like this:
We have a function, f(x) = x2 and we want to take the derivative using the power rule.
Step 1 – Bring down the power and multiply it by the variable’s coefficient. Since the current coefficient is ‘1,’ the new coefficient is simply ‘2.’
Step 2 – Decrease the power of the variable by ‘1,’ making the new power ‘1,’ which doesn’t need to be written.
Therefore, the derivative is 2x. Or f'(x) = 2x
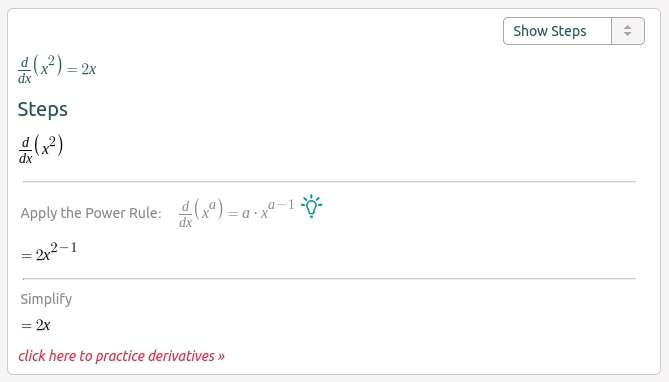
The screenshot above is from Symbolab, a free online derivative calculator that I use to check my work. You can them out by clicking here.
How Do I Use The Derivative?
In Calculus 1, you can also expect to use the derivative in a few different ways. However, in many real-use cases, you’ll have to find not only the first derivative but the second derivative.
What? There’s a second derivative? That’s right. There’s also a third, fourth, fifth, and so on until there’s nothing left of the function. Some functions disappear after it’s been derived a few times while others (trig functions) can be derived infinitesimally.
One of the first ways we apply these derivatives is by analyzing graphs. And if we want to graph a complex function, there are a few things we want to look at:
- Finding the Domain
- Finding the X-intercept(s) & Y-intercept
- Determining the symmetry of the graph
- Determining/Finding asymptotes
- Finding intervals of increment/decrement (Found using the first Derivative)
- Finding local min & max values (Found using the first Derivative and original Function)
- Determining concavity/inflection (Found using the Second Derivative)
- Finally, Draw a rough graph

There are other ways of using derivatives such as optimization, related rates, parametric equations and more. However, this should give you a good idea of what to expect from Calculus 1, as far as Differentiation goes.
The Last 15% – Integrals
Remember earlier when I said you can take the second derivative of a function, the third derivative, and so on? Well, you can also take the Anti-Derivative of a function. This is called the Integral of the function.
Integral = Anti-Derivative
Calculus 2 is Integral Calculus, so it’s a continuation of where you leave off in Calculus 1. That’s why Universities will often spend some time on it at the end of the semester.
How do I find the Integral of a function?
Well, if you use the power rule to find the Derivative of a Function, guess what rule you use to find the Anti-Derivative?
That’s right, it’s the reverse-power rule!
The Reverse-Power Rule
There are two steps to taking the Derivative with the power rule, but the reverse-power rule has three steps. Since we took the derivative of x2 and got 2x, let’s take the Anti-Derivative of 2x.
f(x) = 2x
Step 1 – Increase the power on the variable by ‘1.’
Step 2 – Divide the variable by the new power, which in this case is ‘2.’
Step 3 – Add “+ C” to the end of your new function to signify a constant that would’ve been taken out in a derivative. This may be ‘0’ or it may be ‘1,000.’ All that matters is that you should add the general constant: + C
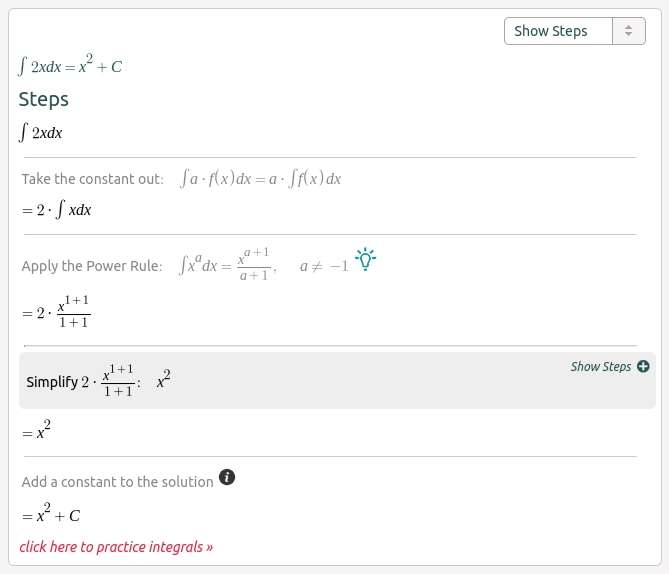
There are, of course, more rules to Integrals than the reverse-power rule. However, this isn’t meant to teach you, just shows you what to expect from Calculus 1. I hope this was helpful!
What To Do If You’re Struggling With Calculus
If you’re struggling in your Calculus class, know that you’re not alone. Calculus can be really difficult, especially is you didn’t learn everything you need to know from your previous courses such as algebra and trigonomotry. If this sounds like you, then I have two articles that will be of help to you.
The first one is How To Pass Calculus In 5 Steps. This walks you through the steps needed in order to pass Calculus in a way that makes it feel easy. Granted, it still takes hard work and dedication. However, if you follow the steps in the guide, it will greatly help you succeed.
The second article is Calculus Resources (Best Books And Websites). This article has my top ten favorite resources that I’ve used while taking Calculus. At times, I’ve been so far behind in class I didn’t know if I was going to pass. The reason was that I just didn’t have a good foundation, there were holes in my math knowledge. These resources helps me close these gaps in my knowledge and helped complete my assignments easier and faster. I highly recommend you read both of these articles.
Final Thoughts
In conclusion, Calculus 1 is a crucial course for any student interested in pursuing a career in science, technology, engineering, mathematics, or any other field that involves quantitative problem-solving. Through this course, students will develop a deep understanding of mathematical concepts and acquire the skills necessary to solve complex problems.
While Calculus 1 can be challenging, with hard work, dedication, and a willingness to learn, any student can succeed in this course. By leveraging the tips and resources provided in this blog post, students can build a strong foundation in calculus and pave the way for future success in their academic and professional careers.
So, if you are ready to dive into the exciting world of calculus, get ready to work hard, push your limits, and discover the incredible power of mathematics.

