How many times have you found yourself sitting in a math class asking: “When is calculus actually used for in real life?” That’s exactly what I thought when I was in high school. Now that I’m at University taking Calculus, I really want to know how it’s useful in real life.
I did some research and found out many different functional uses that Calculus has had since its discovery. Today, you can find Calculus within all manner of sciences such as chemistry, physics, computer science, and engineering, and even business and economics.
What Is Calculus Used For?
Calculus is used for optimization, summation, and predicting trends through modeling change over time. For example, a manufacturer could use Calculus to optimize production costs. Another example is meteorologists using Calculus to predict the weather patterns.
Calculus Uses In Business
In Business, Calculus is mainly used for optimization. This includes maximizing profits, minimizing cost, and maximizing or minimizing production. Also, Calculus can be used to calculate the rate of change in cost or the marginal revenue for an interest-bearing account.
Let’s look at an example of a factory that manufactures and sells dress-shirts. This factory is capable of producing 60,000 dress-shirts per week. However, they want to optimize their production rate in order to minimize their production costs. How many dress-shirts should they produce weekly?
Let C(x) represent the production cost defined by the following function:
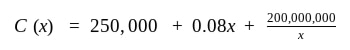
The first thing we want to do is solve for the derivative. Simple enough:
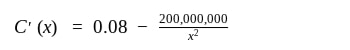
Next, set the derivative equal to zero and solve for x:
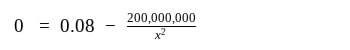
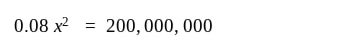
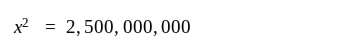
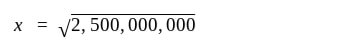
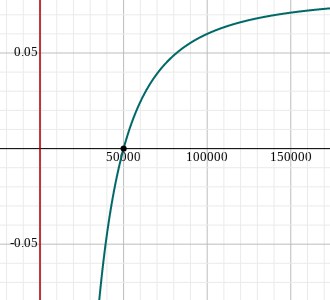
And there we have it! Since there’s no possible way for the factory to make a negative amount of dress-shirts, the optimal number produced is positive. We can see this when we graph the original cost function, C(x). The critical point is the positive x-intercept which as we calculated earlier from C'(x), is 50,000.
Calculus Uses In Engineering
In Engineering, Calculus is mainly used for optimization and summation. This includes the famous Navier-Stokes equations which describe the physical phenomena produced by aircraft. These equations are very useful to Aerospace Engineers.
The Navier-Stokes equations describe the motions of fluid-like substances, such as liquids and gases. This is why they’re so useful in the engineering of aircraft.
However, the Navier-Stokes equations are actually much more versatile, having applications in modeling the motion of stars, weather, pollution, ocean currents, and blood flow.
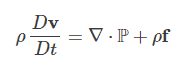
If the equation above looks like an alien language, then you’re not alone. Few people can look at the above and understand the implications, let alone what each of the characters represents and how they relate to each other. Each character represents the following:
ρ = Density of the fluid
v = Velocity of the fluid
Dv / Dt = The derivative of ‘v‘ with respect to time, ‘t‘
∇ (Del) = Gradient of the Vector Field
= (tensor) Surface forces on fluid
= Additional body forces
These equations are typically taught in Calculus 3 (Vector / Multivariable Calculus) and beyond. However, the Navier-Stokes equations aren’t completely solved. The Navier-Stokes existence of smoothness equation is part of the Millenium Prize Problems: 7 unsolved problems that will earn any person $1,000,000 if they solve just one of them.
Read more about the Navier-Stokes equations and the Millenial prize problems here:
Wikipedia: Millenium Prize Problems
How Is Calculus Used In Physics
The applications of Calculus in Physics are abundant. This is because time is virtually always a factor in physics and because modeling change is the primary function of Calculus. The applications include all matter of kinematics, electrodynamics, fluid dynamics, and more.
Let’s look at a basic example of Calculus in kinematics using go-carts.
You’re driving a high-speed go-cart, racing your friend. When you cross the finish line (in 1st place), you hit the brakes and decelerate constantly at 16 feet per second squared. Your go-cart travels 200 feet after you hit the brakes before it finally stops. How fast were you going when you first braked?
First, it’s important to note that there are three functions all dependent on time ‘t’ in this equation: position, velocity, and acceleration. These three functions are related, as they are the derivatives and antiderivatives of each other.
Acceleration (is the derivative of) Velocity (is the derivative of) Position
And the reverse is true, also.
Position (is the antiderivative of) Velocity (is the antiderivative of) Acceleration
Now let’s define these functions and set up our equation.
Let s(t) = Position
Let v(t) = Velocity
Let a(t) = Acceleration
| Braking Begins | Braking Ends |
| Time ‘t’ = 0 | Time ‘t’ = n |
| Position s(0) = 0 | Position s(n) = 200 |
| Velocity v(0) = ? | Velocity v(n) = 0 |
| Acceleration a(0) = -16 | Acceleration a(n) = -16 |
Since we know the Acceleration function a(t) = -16 (we’re decelerating so the acceleration is negative), we can take the antiderivative to find the Velocity function v(t).
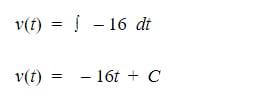
Now, let’s take the antiderivative of our Velocity function to get our Position function.
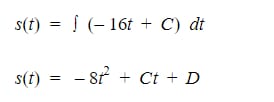
If we consider that at time t=0, the position is 0, we can see that the constant ‘D’ is equal to 0. This leaves us with the following functions for Position and Velocity.
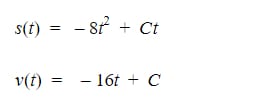
Now let’s solve for ‘n’ (the time it takes to come to a complete stop). We’ll do this by plugging ‘n’ into our equation for our time value and using substitution with these two equations.
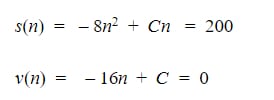
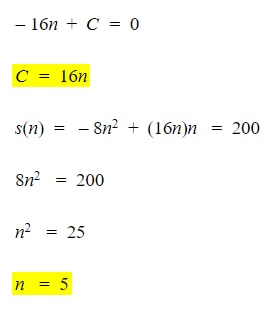
From here, it’s very simple to plug ‘n’ into our other highlighted equation for ‘C’ to reach our final answer. It took 5 seconds to stop and our go-cart was originally going 80 feet per second.
As trivial as calculating the speed of a go-cart might seem, the same mathematical principals can be applied to something more substantial, such as calculating the landing path of a rocket.
Also, as complicated as this calculation may seem, it’s actually very basic. This calculation can be solved by many first-year University students.
How Is Calculus Used In Chemistry
In Chemistry, Calculus is used for modeling reactions, calculating radioactive decay rate, transferring heat, and much more. This includes and extends beyond thermodynamics, electrochemistry, analytical chemistry, and quantum chemistry.
Let’s see how Calculus is used in finding the radioactive decay rate of Uranium 238.
We’ll start by looking at a simple formula:
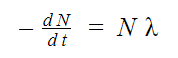
This formula states that, whether I have a large or a small sample of radioactive matter, it will decay at a rate proportional to its size. Because of this, the decay rate actually changes as time goes on and the sample shrinks. This is why Calculus is so useful in determining the decay rate at any given time.
= The number of atoms decaying per second in a given sample
= Number of atoms (size of the sample)
= The decay constant, specific to each radioactive element (Uranium-238 = 
)
Now, knowing the decay constant and using a little calculus, we can come up with our formula to solve for decay rate at any given time. Let’s take our first formula and move our ‘N’ term to one side.
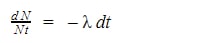
Next, we’ll integrate over a general interval and evaluate said integral.
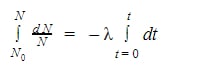
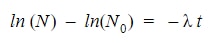
Then, we’ll combine the left side of the equation using log rules.
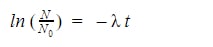
Cancel out the natural log (ln).
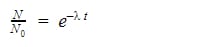
Finally, multiply both sides by 
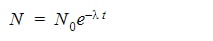
There we have it! We’ve arrived at the formula for radioactive decay, which we could very easily use to solve the half-life of our sample.
Calculus In Computer Science
In Computer Science, Calculus is used for machine learning, data mining, scientific computing, image processing, and creating the graphics and physics engines for video games, including the 3D visuals for simulations. Calculus is also used in a wide array of software programs that require it.
Once you reach Calculus 3, you learn about 3D models using multiple variable equations. One way Computer Science students utilize these models is through game development.
In video game development, Calculus comes into play in major ways:
- 3D graphics and illumination
- Physics engines
As the Physics applications were discussed earlier with the go-cart example, let’s look at the application in 3D graphics and illumination. More specifically, let’s look at spherical harmonics.
Spherical harmonical functions are solutions to the Laplace formula when restricted to a sphere.
How is Calculus used in developing video games?
By using and manipulating Laplace formulas, developers can create a 3D mapping of virtual environments and their textured surfaces. Models are also used to apply appropriate shadows, illumination, and refraction to represent the physical world and the objects that move through it.
Read more about Spherical Harmonics and how they’re used in developing games from Peter-Pike Sloans scholarly article here:
Peter-Pike Sloan: Stupid Spherical Harmonics (SH) Tricks